TRASLACIÓN
Al realizar una traslación , desplazamos una figura a la derecha, la izquierda, hacia arriba o abajo. Esto implica que las coordenadas de los vértices cambiaran. Observa el siguiente diagrama.

Ahora realicemos una traslación de la figura.
Podemos elegir cuantas posiciones y en qué dirección mover el triángulo. Si movemos el triángulo 3 posiciones hacia abajo, todos los vértices del triángulo en el eje y− disminuyen en 3. Esto quiere decir que los pares ordenados de los nuevos vértices cambian. Específicamente, la coordenada y− de cada par disminuye en 3.
Veamos cómo funciona.
¿Has intentado crea runa obra de arte alguna vez? Mira lo que encontró Tanya en el museo.
Tanya encontró un sector en el que podías crear una obra de arte usando un computador. Estas graficas se pueden crear y modificar usando un programa. Tanya uso el programa para crear esta imagen.

Creo una imagen que comenzó en la posición azul y se movió hacia la posición roja.
¿Sabes cómo se les llama a estas dos figuras?
En el plano cartesiano puedes cambiar las figuras de muchas maneras. Esta Sección te enseñara cómo.
Orientación
Al realizar una traslación , desplazamos una figura a la derecha, la izquierda, hacia arriba o abajo. Esto implica que las coordenadas de los vértices cambiaran. Observa el siguiente diagrama.

Ahora realicemos una traslación de la figura.
Podemos elegir cuantas posiciones y en qué dirección mover el triángulo. Si movemos el triángulo 3 posiciones hacia abajo, todos los vértices del triángulo en el eje y− disminuyen en 3. Esto quiere decir que los pares ordenados de los nuevos vértices cambian. Específicamente, la coordenada y− de cada par disminuye en 3.
Veamos cómo funciona.

Podemos notar cómo cambian las coordenadas de y y− . Compara los puntos superiores. El valor de y− original es 2, luego de moverlo cambia a -1. La coordenada y− disminuye en 3. Ahora compara las puntas izquierdas de cada triángulo. El valor de y− original es -2, luego de moverlo cambia a -5. Nuevamente, la coordenada y− disminuye en 3. En el último punto, el valor original de y− es -6, luego de moverlo cambia a -9. En cada punto, la coordenada y− disminuye en 3 mientras que las coordenadas y− es -6, luego de moverlo cambia a -9. En cada punto, la y− disminuye en 3 mientras que las coordenadas x− se mantienen igual. Esto significa que movimos el triángulo 3 posiciones hacia abajo.
Podemos trasladar las figuras de otras maneras también. Podemos mover las figuras hacia la derecha o la izquierda en el plano cartesiano al cambiar sus valores de x− También podemos mover las figuras en diagonal al cambiar sus valores de x− e y− . cambiarán de igual manera.
Para graficar una traslación, debemos realizar el mismo cambio en cada punto.
REFLEXIÓN
También podemos identificar una reflexión por el cambio en sus coordenadas. Recuerda que en una reflexión, la figura gira para crear una imagen reflejo de sí misma. Observa la reflexión de abajo.

Normalmente las figuras se reflejan sobre el eje x− o el eje y− En este caso, la figura se refleja sobre el eje x− . Si comparamos las figuras del primer ejemplo vértice por vértice, veremos que las coordenadas de x− cambiar pero las de y− se mantienen. Esto se debe a que la reflexión se realizó desde la derecha hacia el eje x− Al reflejar sobre el eje y− las coordenadas de y− cambian y las de x− se mantienen. Mira este ejemplo:
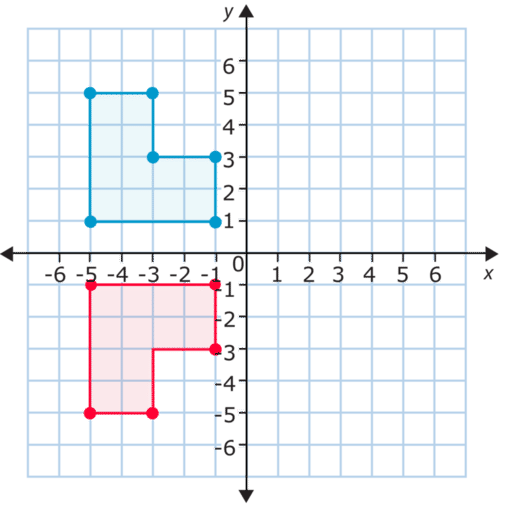
Comparemos algunos de los vértices. En la figura de arriba las coordenadas para el vértice superior izquierdo de la figura original son (-5, 5). Al reflejar la figura sobre el eje
y− las coordenadas del vértice correspondiente son (-5, -5). ¿Cuáles son las coordenadas del vértice inferior derecho? Las coordenadas originales son (-1, 1) y luego de reflejarla las coordenadas cambian a (-1, -1). Como puedes apreciar solo las coordenadas de x− cambian. De hecho, las coordenadas de y− se convierten en enteros negativos de las originales Esto indica que se trata de una reflexión vertical (arriba/abajo) o una reflexión sobre el eje x− .
En una reflexión horizontal (izquierda/derecha) o una reflexión sobre el eje y− las coordenadas de x− cambian a enteros negativos. Veamos el siguiente ejemplo.
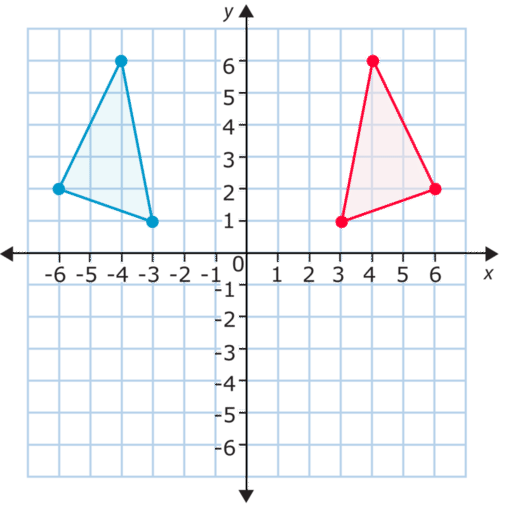
Esta es una reflexión sobre el eje x− Compara los puntos. Notas como las coordenadas de y− se mantienen iguales. Las coordenadas de x− se convierten en enteros negativos de las originales. Mira la punta superior del triángulo, por ejemplo. Las coordenadas del punto original son (-4, 6) y las coordenadas del punto nuevo son (4, 6). La coordenada x− cambió de -4 a 4.
Podemos reconocer reflexiones por estos cambios en las coordenadas x− o y− Si reflejamos sobre el eje x− las coordenadas de x− cambiarán a negativas. Si reflejamos sobre el eje y− las coordenadas de y− cambiarán a negativas.
También podemos usar esta información para graficar reflexiones. Para graficar una reflexión, debemos decidir si será sobre el eje x− o y− y cambiar las coordenadas de x− o y−
ROTACION
Ahora grafiquemos el tercer tipo de transformación: La rotación. Una rotación es una transformación que gira la figura en sentido del reloj o contra el reloj. La figura de abajo ha sido rotada. ¿Cuáles son sus coordenadas nuevas?

Las coordenadas nuevas de los vértices del rectángulo son (1, -3), (1, 2), (3, 2) y (3, -3). En este caso, tanto las coordenadas de x− como las de y− cambiaron. A diferencia de una traslación o reflexión, una rotación cambiar ambas coordenadas de un par ordenado. Ahora observa con atención. ¡Uno de los puntos no cambió! Eso se debe a que la figura rotó en ese punto. Imagina que pones tu dedo en esa esquina del rectángulo y lo haces girar. Eso sucede con las rotaciones. El rectángulo rotó 90∘ en el sentido del reloj.
¿Cómo graficamos una rotación?
Al graficar una rotación, primero debemos saber cuánto rotará la figura. Al rotar el rectángulo de arriba en 90∘ , este queda en posición vertical. Al rótalo en 180∘ vuelve a quedar horizontal. También debemos saber sobre qué punto se rotará. Este es el punto que se mantendrá igual.
Luego, debemos contar cuánto mide la figura. La figura de arriba se extiende del 1 al -4 en eje x− Ese es un total de 5 unidades a lo largo del eje x− Al rotar una figura en 90∘ la distancia en el eje x− se convierte en la distancia en el eje y− Mira el rectángulo. Los lados largos son horizontales en la figura original, pero luego de rotarla los lados largos quedan en posición vertical. Esto quiere decir que la distancia en x− de 5 se convierte en la distancia en y− de 5.
Recuerda que el punto (1, 3) se mantiene igual, así que es una esquina de la figura nueva. Debemos sumar 5 a la coordenada de y− para encontrar el siguiente vértice del rectángulo. −3+5=2 . Entonces el otro vértice estaría en las coordenadas (1, 2).
Para encontrar los otros puntos del rectángulo rotado, debemos considerar su ancho también. Primero, encuentra el ancho, o el lado corto, del rectángulo original. El rectángulo ocupa 2 unidades en el eje y− Al rotar la figura, este ancho se convierte en el ancho para el eje x− En otras palabras, debemos sumar 2 a la coordenada de x− del punto que no se mueve. 1+2=3 , de esta manera el vértice del rectángulo será (3, -3). Para encontrar el último vértice, suma 2 a la coordenada de x− del otro par ordenado que conocemos, (1, 2). El último vértice se encuentra en la coordenada (3, 2)







